The Mathematics of Galilean Viewfinders and How to Design them
Viewfinders & Rangefinders > The Mathematics of Galilean Viewfinders and How to Design them
Galilean viewfinders are the dominant design found in vintage and modern cameras, this is because it is a relatively simple two piece design, consisting of a front plano-concave (PCV) element, and a rear, plano-convex (PCX), or dual-convex (DCX) lens. The idea behind the design is to create an afocal system, this means that the effective focal length of the assembly is infinite, so the rays end up parallel after exiting the assembly, the light is collimated and magnification is reduced (if you reverse the design you create a Galilean telescope, increasing magnification).
Let the front PCV element be of focal length f1, and the rear PCX or DCX element be of focal length f2. The magnification of the viewfinder will be:
m = |f1|/|f2|
To make an afocal system, you want the distance in between the elements to be equal to the focal lengths of the elements added to each other:
d=f1+f2
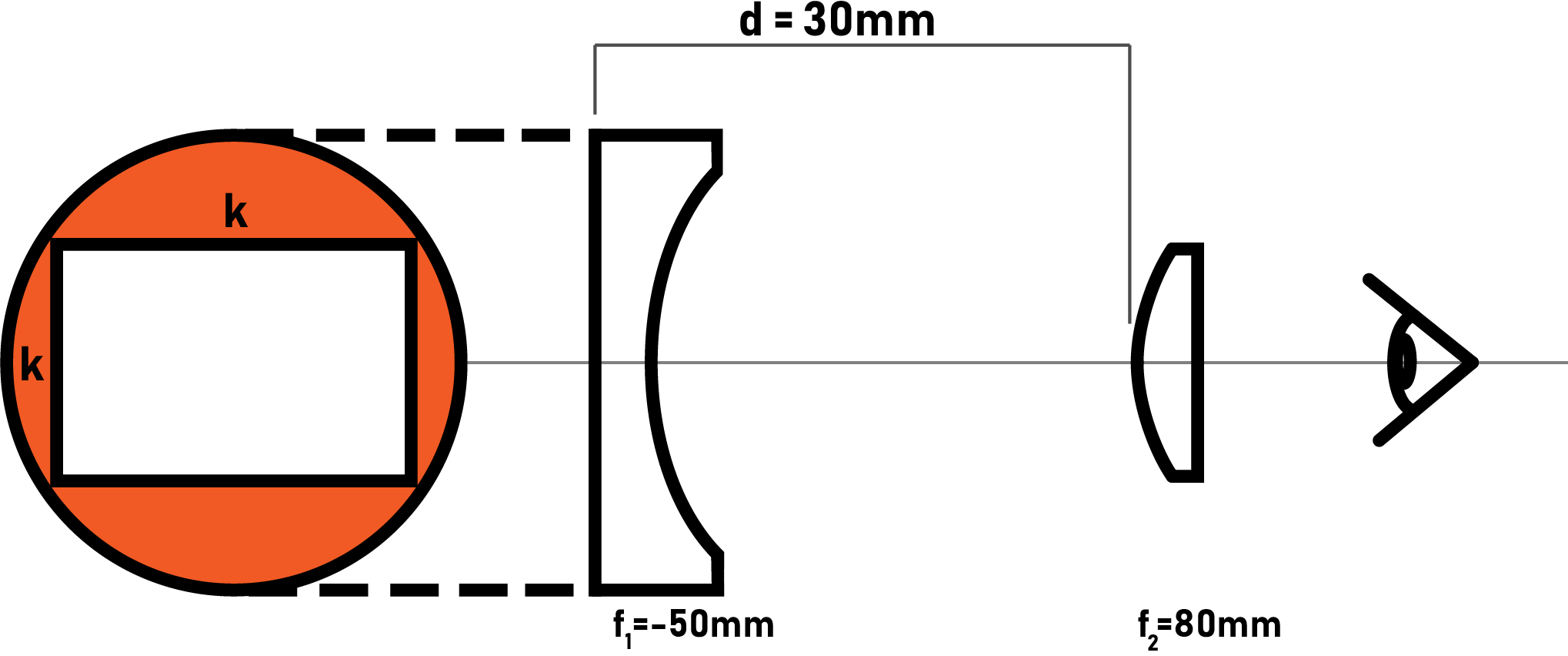
Let’s take an example, in a galilean viewfinder, where the front PCV element is of negative focal length -50mm, and the rear element is PCX or DCX, of positive focal length 80mm, the distance in between would be equal to:
d=(-50mm) + 80mm = 30mm
The magnification is equal to :
m= |f1|/|f2| = 50/80= 0.625
Note: The focal length to be used is the Front Focal length of the optical element, some suppliers don’t give you that measurement, luckily, Edmund Optics has a handy Focal Length Calculator that will.
So, now you have an afocal system, but to calculate how big it has to be, and how big the frame for your given lens is within that system have to be, the following formula can be used:
k = (j·m·d)/f
where k is one of the dimensions of your frame (length or height, depends on j)
j is either the height or length of your film gate, the output will be the respective frame side size k
m is the magnification
d is the distance between your two elements
f is the focal length of the lens you are intending to use.
if the viewfinder described previously would be used for a 50mm lens on a camera with a standard 24x36mm film gate, then the front frame has to be of dimension :
k_length = (36mm · 0.625 · 30mm )/50mm = 13.5mm
k_height = (24mm · 0.625 · 30mm )/50mm = 9mm
If you’re buying off-the-shelf glass, then it will most likely be round, so using Pythagoras, the diagonal of the frame will be ≈ 16.22mm. This is the smallest piece of glass you can use, unless you’re fine with not having 100% coverage.
All of this math means that you can calculate the focal lengths used for any other galilean viewfinder, if you just know it’s focal length and the distance between the two elements. It also proves that it is not possible to have a viewfinder of magnification 1x because if:
m = f1/f2 = 1
then
f1 = f2
thus
d = 0
so any camera touting a 1x viewfinder, is really just a peep-hole with the correct sized frame.
To make accurate sports finders, just use the frame formula with m=1.
If you think I’ve made a mistake, or something isn’t clear, don’t hesitate to send me an email and I will do my best to address it.
Further Reading :